Image sensor format
In digital photography, the image sensor format is the shape and size of the image sensor.
The image sensor format of a digital camera determines the angle of view of a particular lens when used with a particular camera. In particular, image sensors in digital SLR cameras tend to be smaller than the 24 mm x 36 mm image area of full-frame 35 mm cameras, and therefore lead to a narrower angle of view.
Lenses produced for 35 mm film cameras may mount well on the digital bodies, but the larger image circle of the 35 mm system lens allows unwanted light into the camera body, and the smaller size of the image sensor compared to 35 mm format results in cropping of the image compared to the results produced on the film camera. This latter effect is known as field-of-view crop; the format size ratio is known as the field of view crop factor, crop factor for short, or focal-length multiplier.
Contents |
Sensor size and depth of field
Three possible depth of field comparisons between formats are discussed, applying the formulae derived in the article on depth of field. Considering the case with the same subject distance and angle of view for both formats,
so the DOFs are in inverse proportion to the absolute aperture diameters 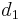 and
and 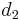 . Using the same absolute aperture diameter for both formats with the “same picture” criterion (equal angle of view, magnified to same final size) is equivalent to adjusting the f-number in proportion to crop factor. This means that if the shutter speed is fixed the exposure is changed by the adjustment of the f-number required to equalise depth of field, (f-number being reduced inversely with the crop factor, and aperture area as the square of the crop factor). Since the sensor area increases as the square of the crop factor, at equal depth of field and the same shutter speed all sensors receive the same light flux, whatever their size.
. Using the same absolute aperture diameter for both formats with the “same picture” criterion (equal angle of view, magnified to same final size) is equivalent to adjusting the f-number in proportion to crop factor. This means that if the shutter speed is fixed the exposure is changed by the adjustment of the f-number required to equalise depth of field, (f-number being reduced inversely with the crop factor, and aperture area as the square of the crop factor). Since the sensor area increases as the square of the crop factor, at equal depth of field and the same shutter speed all sensors receive the same light flux, whatever their size.
Alternatively, we might compare the depth of field of sensors receiving the same photometric exposure. In that case, with a fixed shutter speed the ratio of depths of field is given as
where 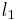 and
and 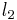 are the characteristic dimensions of the format, and thus
are the characteristic dimensions of the format, and thus 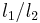 is the relative crop factor between the sensors. It is this result that gives rise to the common opinion that small sensors yield greater depth of field than large ones.
is the relative crop factor between the sensors. It is this result that gives rise to the common opinion that small sensors yield greater depth of field than large ones.
A third alternative is to consider the depth of field given by the same lens in conjunction with different sized sensors. The change in depth of field is brought about by the requirement for a different degree of enlargement to achieve the same final image size. In this case the ratio of depths of field becomes
Sensor size, noise and dynamic range
Discounting pixel response non-uniformity (PRNU), which is not sensor size dependent, the noises in an image sensor are photon shot noise, read noise and dark noise. The overall signal to noise ratio of a sensor (SNR), observed at the scale of a single pixel, is

where  is the incident photon flux (photons per second in the area of a pixel),
is the incident photon flux (photons per second in the area of a pixel), 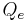 is the quantum efficiency,
is the quantum efficiency,  is the exposure time,
is the exposure time,  is the pixel dark current in electrons per second and
is the pixel dark current in electrons per second and 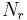 is the pixel read noise in electrons[1].
is the pixel read noise in electrons[1].
Each of these noises has a different dependency on sensor size.
Exposure and photon flux
Image sensor noise can be compared across formats for a given fixed photon flux per pixel area (the P in the formulas); this analysis is useful for a fixed number of pixels with pixel area proportional to sensor area, and fixed absolute aperture diameter for a fixed imaging situation in terms of depth of field, diffraction limit at the subject, etc. Or it can be compared for a fixed focal-plane illuminance, corresponding to a fixed f-number, in which case P is proportional to pixel area, independent of sensor area. The formulas above and below can be evaluated for either case.
Shot noise
In the above equation, the shot noise SNR is given by 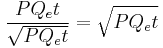
Apart from the quantum efficiency it depends on the incident photon flux and the exposure time, which is equivalent to the exposure and the sensor area, since the exposure is the integration time times the image plane illuminance, and illuminance is the luminous flux per unit area. Thus for equal exposures, the signal to noise ratios of two different size sensors of equal quantum efficiency and pixel count will (for a given final image size) be in proportion to the square root of the sensor area (or the linear scale factor of the sensor). If the exposure is constrained by the need to achieve some required depth of field (with the same shutter speed) then the exposures will also be in relation to the square root of the sensor area, producing the interesting result that if depth of field is a constraint, image shot noise is not dependent on sensor area.
Read noise
The read noise is the total of all the electronic noises in the conversion chain for the pixels in the sensor array. To compare it with photon noise, is must be referred back to its equivalent in photoelectrons, which requires the division of the noise measured in volts by the conversion gain of the pixel. This is given, for an active pixel sensor, by the voltage at the input (gate) of the read transistor divided by the charge which generates that voltage, 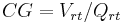 . This is the inverse of the capacitance of the read transistor gate (and the attached floating diffusion) since capacitance
. This is the inverse of the capacitance of the read transistor gate (and the attached floating diffusion) since capacitance  [2]. Thus
[2]. Thus 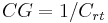 .
.
In general for a planar structure such as a pixel, capacitance is proportional to area, therefore the read noise scales down with sensor area, as long as pixel area scales with sensor area, and that scaling is performed by uniformly scaling the pixel.
Considering the signal to noise ratio due to read noise at a given exposure, the signal will scale as the sensor area along with the read noise and therefore read noise SNR will be unaffected by sensor area. In a depth of field constrained situation, the exposure of the larger sensor will be reduced in proportion to the sensor area, and therefore the read noise SNR will reduce likewise.
Dark noise
The dark current contributes two kinds of noise: dark offset, which is only partly correlated between pixels, and the shot noise associated with dark offset, which is uncorrelated between pixels. Only the shot-noise component Dt is included in the formula above, since the uncorrelated part of the dark offset is hard to predict, and the correlated or mean part is relatively easy to subtract off. The mean dark current contains contributions proportional both to the area and the linear dimension of the photodiode, with the relative proportions and scale factors depending on the design of the photodiode.[3] Thus in general the dark noise of a sensor may be expected to rise as the size of the sensor increases. However, in most sensors the mean pixel dark current at normal temperatures is small, lower than 50 e- per second,[4] thus for typical photographic exposure times dark current and its associated noises may be discounted. At very long exposure times, however, it may be a limiting factor. And even at short or medium exposure times, a few outliers in the dark-current distribution may show up as "hot pixels".
Dynamic range
Dynamic range is the ratio of the largest and smallest recordable signal, the smallest being typically defined by the 'noise floor'. In the image sensor literature, the noise floor is taken as the readout noise, so 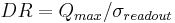 [5] (note, the read noise
[5] (note, the read noise 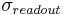 is the same quantity as
is the same quantity as 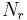 referred to in [1])
referred to in [1])
The measurement here is made at the level of a pixel (which strictly means that the DR of sensors with different pixel counts is measured over a different spatial bandwidth, and cannot be compared without normalisation). If we assume sensors with the same pixel count but different sizes, then the pixel area will be in proportion to the sensor area. If the maximum exposure (amount of light per unit area) is the same then both the maximum signal and the read noise reduce in proportion to the pixel (and therefore the sensor) area, so the DR does not change. If the comparison is made according to DOF limited conditions, so that the exposure of the larger sensor is reduced in proportion to the area of the sensor (and pixel, for sensors with equal pixel count) then 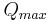 is constant, and the read noise (
is constant, and the read noise (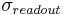 ) falls with the sensor area, leading to a higher dynamic range for the smaller sensor. Summarising the above discussion, considering separately the parts of the image signal to noise ratio due to photon shot noise and read noise and their relation to the linear sensor size ratio or 'crop factor' (remembering that conventionally crop factor increases as the sensor gets smaller) then:
) falls with the sensor area, leading to a higher dynamic range for the smaller sensor. Summarising the above discussion, considering separately the parts of the image signal to noise ratio due to photon shot noise and read noise and their relation to the linear sensor size ratio or 'crop factor' (remembering that conventionally crop factor increases as the sensor gets smaller) then:
| Shot noise SNR | Read noise SNR | Dynamic range | |
|---|---|---|---|
| Fixed exposure | Inversely proportional to crop factor | No change | No change |
| DOF constrained | No change | Proportional to square of crop factor | Proportional to square of crop factor |
It should be noted that this discussion isolates the effects of sensor scale on SNR and DR, in reality there are many other factors which affect both these quantities.
Sensor size and diffraction
The resolution of all optical systems is limited by diffraction. One way of considering the effect that diffraction has on cameras using different sized sensors is to consider the modulation transfer function (MTF) due to diffraction, which will contribute a factor to the overall system MTF along with the other factors, typically the MTFs of the lens, anti-aliasing filter and sensor sampling window [6]. The spatial cut-off frequency due to diffraction through a lens aperture is
where λ is the wavelength of the light passing through the system and N is the f-number of the lens. If that aperture is circular, as are (approximately) most photographic apertures, then the MTF is given by
for 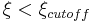 and
and 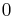 for
for 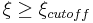 [7] The diffraction based factor of the system MTF will therefore scale according to
[7] The diffraction based factor of the system MTF will therefore scale according to 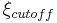 and in turn according to
and in turn according to 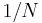 (for the same light wavelength).
(for the same light wavelength).
In considering the effect of sensor size, and its effect on the final image, the different magnification required to obtain the same size image for viewing must be accounted for, resulting in an additional scale factor of 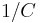 where
where 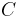 is the relative crop factor, making the overall scale factor
is the relative crop factor, making the overall scale factor 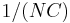 . Considering the three cases above:
. Considering the three cases above:
For the 'same picture' conditions, same angle of view, subject distance and depth of field, then the F-numbers are in the ratio 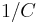 , so the scale factor for the diffraction MTF is 1, leading to the conclusion that the diffraction MTF at a given depth of field is independent of sensor size.
, so the scale factor for the diffraction MTF is 1, leading to the conclusion that the diffraction MTF at a given depth of field is independent of sensor size.
In both the 'same photometric exposure' and 'same lens' conditions, the F-number is not changed, and thus the spatial cutoff and resultant MTF on the sensor is unchanged, leaving the MTF in the viewed image to be scaled as the magnification, or inversely as the crop factor.
Sensor format and lens size
It might be expected that lenses appropriate for a range of sensor sizes could be produced by simply scaling the same designs in proportion to the crop factor.[8] Such an exercise would in theory produce a lens with the same F-number and angle of view, with a size proportional to the sensor crop factor. In practice, simple scaling of lens designs is not always achievable, due to factors such as the non-scalability of manufacturing tolerance, structural integrity of glass lenses of different sizes and available manufacturing techniques and costs. Moreover, to maintain the same absolute amount of information in an image (which can be measured as the space bandwidth product[9]) the lens for a smaller sensor requires a greater resolving power. The development of the 'Tessar' lens is discussed by Nasse[10], and shows its transformation from an f/6.3 lens for plate cameras using the original three-group configuration through to an f/2.8 5.2 mm four-element optic with eight extremely aspheric surfaces, economically manufacturable because of its small size. Its performance is 'better than the best 35 mm lenses – but only for a very small image'.
In summary, as sensor size reduces, the accompanying lens designs will change, often quite radically, to take advantage of manufacturing techniques made available due to the reduced size. The functionality of such lenses can also take advantage of these, with extreme zoom ranges becoming possible. These lenses are often very large in relation to sensor size, but with a small sensor can be fitted into a compact package.
Sensor size and telecentricity
Images incident on image sensors should be made up of rays hitting photoreceptors fairly close to perpendicular, for best detection efficiency and low pixel crosstalk. Lenses that produce such near-perpendicular incident angles, i.e. with rear elements farther away from the sensor for a given focal length, are said to be "image-side telecentric". As the lens designer moves a lens' rear elements farther away from the sensor, to achieve a more telecentric lens, they must package the lens elements in increasingly long and bulky housings.
Smaller pixel size, smaller sensors tend to be affected more noticeably by the non-perpendicularity of light coming from less-telecentric lenses. The result of this relatively high telecentricity sensitivity is that lenses for sensors that are half the size of a larger format, cannot always be designed with rear elements twice as close to the sensor. Consider a 40mm focal length lens for a 36mm width sensor, that might function without corner smearing or corner color shifts with a rear lens element that is 30mm away from the sensor. One might think that the rear element of 4mm focal length lens working with a 3.6mm width sensor could similarly be designed with a rear element that is just 3mm from the sensor.
However the net result of the increased telecentricity sensitivity of smaller sensors, is that the lenses that work well with them must have rear elements that are relatively farther away from the sensor than their smaller focal length suggests. Thus small-sensor lenses are housed in packages that are physically longer than one would predict from looking at the housings of lenses for larger sensors.
Film cameras did not have such sensitivity to the angle of light striking the film surface, since film is sensitive to light regardless of its direction or incident angle. That is possibly the main reason why there were 24×36 mm (full-frame) compact-zoom film cameras whose lenses were much smaller (i.e. with closer rear elements) than typical digital zoom lenses for 24×36mm sensors.
Common image sensor formats
DSLR/MILC formats
Some professional DSLRs use full-frame sensors, equal to the size of a frame of 35 mm film.
Most consumer-level DSLRs and MILCs/EVILs use relatively large sensors, either around the size of a frame of APS-C film, with a crop factor of 1.5-1.6; or 30% smaller than that, with a crop factor of 2.0 (this is the Four Thirds System, adopted by Olympus and Panasonic).
On September 21, 2011, Nikon announced a new format, which they named CX.[11] It will be adopted for the Nikon 1 camera system (Nikon J1 and V1 models). The sensor size of the CX format is 1" (2.7 crop factor).
As of September 2011[update] there was only one MILC model equipped with a very small sensor, the Pentax Q with a 1/2.3" sensor (5.62 crop factor) size more typical of compact digital cameras. See Compact digital camera formats section below.
Many different terms are used in marketing and describing these sensor formats, including the following:
- Full-frame digital SLR format, with sensor dimensions nearly equal to those of 35 mm film (36 × 24 mm)
- Canon's APS-H format for high-speed pro-level DSLRs (crop factor 1.3)
- Leica's M8 and M8.2 sensor (crop factor 1.33).
- APS-C refers to a range of similarly-sized formats, including
- Nikon DX format, Pentax, Konica Minolta/Sony α, Fuji (crop factor 1.5)
- Canon entry-level DSLR formats (crop factor 1.6)
- Foveon X3 format used in Sigma SD-series DSLRs (crop factor 1.7)
- Four Thirds System format (crop factor 2.0)
- Nikon CX format used in Nikon 1 series (crop factor 2.7)
Production costs for a full frame sensor can exceed twenty times the costs of an APS-C sensor. Only about thirty full-frame sensors can be produced on an 8 inches (20 cm) silicon wafer that would fit 112 APS-C sensors, and there is a significant reduction in yield due to the large area for contaminants per component. Additionally, the full frame sensor requires three separate exposures during the photolithography stage, which requires separate masks and quality control steps. The APS-H size was selected since it is the largest that can be imaged with a single mask to help control production costs and manage yields.[12]
Due to the ever-changing constraints of semiconductor fabrication and processing, and because camera manufacturers often source sensors from third-party foundries, it is common for sensor dimensions to vary slightly within the same nominal format. For example, the Nikon D3 and D700 cameras' nominally full-frame sensors actually measure 36 × 23.9 mm, slightly smaller than a 36 × 24 mm frame of 35 mm film. As another example, the Pentax K200D's sensor (made by Sony) measures 23.5 × 15.7 mm, while the contemporaneous K20D's sensor (made by Samsung) measures 23.4 × 15.6 mm.
Most DSLR image sensor formats approximate the 3:2 aspect ratio of 35 mm film. Again, the Four Thirds System is a notable exception, with an aspect ratio of 4:3 as seen in most compact digital cameras (see below).
Medium-format DSLR
The most common sensor size for medium-format digital cameras is approximately 48 × 36 mm (1.9 × 1.4 in), due to the widespread use of Kodak's 22-megapixel KAF-22000 and 39-megapixel KAF-39000[13] CCDs in that format. Phase one offers the P65+ digital back with Dalsa's 53.9 × 40.4 mm (2.12 × 1.59 in) 16-bit sensor containing 60.5 megapixels[14] and Leica offers an "S-System" DSLR with a 45 × 30 mm (1.8 × 1.2 in) sensor containing 37-megapixels.[15] In 2010, Pentax released the 40MP 645D medium format DSLR with a 44 × 33 mm (1.7 × 1.3 in) sensor.[16]
Compact digital camera formats
The sensor sizes of many compact digital cameras are expressed in terms of the non-standardized "inch" system, as approximately 1.5 times the length of the diagonal of the sensor. This goes back to the way image sizes of early video cameras were expressed in terms of the outside diameter of the glass envelope of the video camera tube. David Pogue of the New York Times states that "the actual sensor size is much smaller than what the camera companies publish — about one-third smaller." For example, a camera advertising a 1/2.7" sensor does not have a sensor with a diagonal of 0.37"; instead, the diagonal is closer to 0.26".[17][18] Instead of "formats", these sensor sizes are often called types, as in "1/2-inch-type CCD." Most compact image sensors have an aspect ratio of 4:3. This matches the aspect ratio of the popular VGA, SVGA, and XGA display resolutions, allowing images to be displayed on most computer monitors without cropping.
As of December 2010[update] most compact digital cameras used 1/2.5" or 1/2.3" size sensors. Digicams with the 1/2.5" sensor size include the Panasonic Lumix DMC-FZ18, Canon PowerShot A570 IS, Canon SD870 IS Digital ELPH (IXUS 860 IS), Canon Powershot SX210-IS, Sony Cyber-shot DSC-W80, Canon Powershot S5is, Sony Cyber-shot DSC-H7, Canon PowerShot TX1, Sony Cyber-shot DSC-H9, and Casio Exilim EX-V7. 1/2.3"-sensor digicams include the Kodak Easyshare M530, the Canon Powershot SX130 IS, the Fuji Finepix Z70, and the Nikon Coolpix S8100.
As of 2011[update] many megazoom digicams, including the Pentax Optio X90, the Olympus SP600uz, and the Kodak Z981, used 1/2.33" sensors. Additionally, some Sony digicams used a 1/2.4" sensor size, including the Sony Cyber-shot HX5V.
Compact cameras using sensors of nearly twice the area included Fujifilm Finepix s6000fd/ s6500fd (1/1.7"), Fuji Finepix F50fd (1/1.6") and Finepix F31fd (1/1.7"), Canon PowerShot G12 (1/1.7") and Powershot SD950 IS and S90/S95(1/1.7"), Ricoh Caplio GX100 (1/1.75"), Nikon Coolpix P5000 (1/1.8") and Coolpix P7000 (1/1.7"), some Panasonic Lumix cameras such as the DMC-LX3 and LX5 and the Olympus camera XZ-1(1/1.63"). Fuji announced in September 2011 that their X-10 would have a 2/3" sensor, the largest on a compact camera at the time.
The sensors of camera phones are smaller than those of typical compact cameras, allowing greater miniaturization of the electrical and optical components. Sensor sizes of around 1/6" are common in camera phones, webcams and digital camcorders. The Nokia N8's 1/1.83" sensor was the largest in a phone in late 2011.
Table of sensor sizes
Inch-based sensor formats are not standardized. Originally, they were the outer diameters of the image tubes used in television cameras until the late 1980s. Exact dimensions may vary, but those listed are typical.[18] The listed sensor areas span more than a factor of 1000 and are proportional to the maximum possible collection of light and image resolution (same lens speed, i.e. maximum aperture), but in practice are not directly proportional to image noise or resolution due to other limitations. See comparisons.[19][20]
| Type | Diagonal (mm) | Width (mm) | Height (mm) | Area (mm2) | Stops (Area) | Crop factor[21] |
|---|---|---|---|---|---|---|
| 1/10" | 1.60 | 1.28 | 0.96 | 1.23 | ?? | ?? |
| 1/8" | 2.00 | 1.60 | 1.20 | 1.92 | -8.81 | 21.65 |
| 1/6" | 3.00 | 2.40 | 1.80 | 4.32 | -7.64 | 14.14 |
| 1/4" | 4.00 | 3.20 | 2.4 | 7.68 | -6.81 | 10.83 |
| 1/3.6" | 5.00 | 4.00 | 3.00 | 12.0 | -6.16 | 8.65 |
| 1/3.2" | 5.68 | 4.54 | 3.42 | 15.50 | -5.80 | 7.61 |
| 1/3" | 6.00 | 4.80 | 3.60 | 17.30 | -5.64 | 7.21 |
| 1/2.7" | 6.72 | 5.37 | 4.04 | 21.70 | -5.31 | 6.44 |
| 1/2.5" | 7.18 | 5.76 | 4.29 | 24.70 | -5.12 | 6.02 |
| 1/2.3" | 7.70 | 6.16 | 4.62 | 28.50 | -4.92 | 5.62 |
| 1/2" | 8.00 | 6.40 | 4.80 | 30.70 | -4.81 | 5.41 |
| 1/1.8" | 8.93 | 7.18 | 5.32 | 38.20 | -4.50 | 4.84 |
| 1/1.7" | 9.50 | 7.60 | 5.70 | 43.30 | -4.32 | 4.55 |
| 1/1.6" | 10.07 | 8.08 | 6.01 | 48.56 | -4.15 | 4.3 |
| 2/3" | 11.00 | 8.80 | 6.60 | 58.10 | -3.89 | 3.93 |
| Super 16mm | 14.54 | 12.52 | 7.41 | 92.80 | -3.22 | 2.97 |
| Nikon CX | 15.86 | 13.20 | 8.80 | 116 | -2.90 | 2.81 |
| 1" | 16.00 | 12.80 | 9.60 | 123 | -2.81 | 2.73 |
| m4/3 · 4/3" (Four Thirds) | 21.60 | 17.30 | 13 | 225 | -1.94 | 2.00 |
| Sigma Foveon X3 | 24.90 | 20.70 | 13.80 | 286 | -1.60 | 1.74 |
| Canon APS-C | 26.70 | 22.20 | 14.80 | 329 | -1.39 | 1.62 |
| General APS-C (Nikon, Pentax, Sony/Minolta, Samsung) | 28.2-28.4 | 23.6-23.7 | 15.60 | 368-370 | -1.23 | 1.52-1.54 |
| Canon APS-H | 33.50 | 27.90 | 18.60 | 519 | -0.73 | 1.29 |
| 35mm Full-frame, Nikon D3, Nikon D700 | 43.2-43.3 | 36 | 23.9-24.3 | 860-864 | 0 | 1.0 |
| Leica S2 | 54 | 45 | 30 | 1350 | +0.64 | 0.80 |
| Pentax 645D | 55 | 44 | 33 | 1452 | +0.75 | 0.78 |
| Kodak KAF 39000 CCD[22] | 61.30 | 49 | 36.80 | 1803 | +1.06 | 0.71 |
| Leaf AFi 10 | 66.57 | 56 | 36 | 2016 | +1.22 | 0.65 |
| Phase One P 65+, IQ160, IQ180 | 67.40 | 53.90 | 40.40 | 2178 | +1.33 | 0.64 |
Bridging the gap in sensor sizes
From 2005 there was increasing interest in producing medium-sized cameras with large sensors but without the moving mirror systems, and consequently the bulk, typical of DSLR camera bodies.
Manufacturers gradually responded to this interest. Epson, an early entrant, introduced the R-D1, a digital rangefinder using the Leica M mount. Other companies followed suit, by introducing similar cameras that focus electronically rather than manually (such as Olympus, with its PEN series; Panasonic, with its G and GF series; Sony, with its Nex series; Samsung, with its NX series). Such cameras might overall look like compact digital ones, with at least two notable differences: a sensor in most cases of the size found in digital SLRs, and interchangeable lenses. The latter feature was later incorporated in at least one small-sensor compact camera as well (Pentax Q, announced on June 2011).
Until 2011 there was a large gap in sensor size between digital compact cameras on the one hand and DSLRs/MILCs on the other. Compact cameras were all equipped with sensors smaller than 1/1.6" (48.5 mm2), whereas 4/3" (225 mm2) was the smallest sensor to be found on DSLRs/MILCs. One noticeable exception was the Olympus E-10 (a large, semi-professional hybrid camera announced in the year 2000 and equipped with a comparatively tiny 2/3" sensor). The main reason for the gap was portability: large sensors require bulky lenses (see previous section). Consequently MILC cameras with large sensors tend to show a marked disproportion between their tiny bodies and their large lens systems, especially their zoom objectives.
The size gap was bridged by camera models announced in September 2011. On the compact side of the gap, a very large (for a compact) 2/3" (58.1 mm2) sensor equipped the high-end Fuji X10 compact announced in September. At the same time, on the DSLR/MILC side of the divide, Nikon announced in September the Nikon 1 system, built around a new sensor format they named 'CX' (13.2mm × 8.8mm, roughly 1" in the inch system).
Such format additions, the 'CX' especially, eliminated the previous gap in sensor sizes: the crop-factor difference between the largest compact camera sensor (2/3", 3.9 crop factor) and the smallest MILC sensor (1", 2.7 crop factor) becoming about half the previous gap between 1/1.6" and 4/3" sensors.
See also
Notes and references
- ^ a b Fellers, Thomas J.; Davidson, Michael W.. "CCD Noise Sources and Signal-to-Noise Ratio". Hamamatsu Corporation. http://learn.hamamatsu.com/articles/ccdsnr.html. Retrieved 17 December 2011.
- ^ Aptina Imaging Corporation. "Leveraging Dynamic Response Pixel Technology to Optimize Inter-scene Dynamic Range". Aptina Imaging Corporation. http://www.aptina.com/products/technology/DR-Pix_WhitePaper.pdf. Retrieved 17 December 2011.
- ^ Loukianova, Natalia V.; Folkerts, Hein Otto; Maas, Joris P. V.; Verbugt, Joris P. V.; Daniël W. E. Mierop, Adri J.; Hoekstra, Willem; Roks, Edwin and Theuwissen, Albert J. P. (January 2003). "Leakage Current Modeling of Test Structures for Characterization of Dark Current in CMOS Image Sensors". IEEE Transactions on Electron Devices 50 (1): 77-83. doi:10.1109/TED.2002.807249. http://www.harvestimaging.com/pubdocs/073_2003_jan_TED_leakage_current.pdf. Retrieved 17 December 2011.
- ^ Apogee Imaging Systems. "Dark Count". Apogee Imaging Systems. http://www.ccd.com/ccd109.html. Retrieved 17 December 2011.
- ^ Kavusi, Sam; El Gamal, Abbas (2004). "Quantitative Study of High Dynamic Range Image Sensor Architectures". Proc. of SPIE-IS&T Electronic Imaging 5301: 264-275. http://www-isl.stanford.edu/groups/elgamal/abbas_publications/C099.pdf. Retrieved 17 December 2011.
- ^ Osuna, Rubén & García, Efraín. "Do Sensors “Outresolve” Lenses?". The Luminous Landscape. http://www.luminous-landscape.com/tutorials/resolution.shtml. Retrieved 21 December 2011.
- ^ Boreman, Glenn D. (2001). Modulation Transfer Function in Optical and Electro-Optical Systems. SPIE Press. pp. 120. ISBN 9780819441430. http://spie.org/x34304.xml.
- ^ Ozaktas, Haldun M; Urey, Hakan and Lohmann, Adolf W. (1994). "Scaling of diffractive and refractive lenses for optical computing and interconnections". Applied Optics 33 (17): 3782-3789. doi:10.1364/AO.33.003782.
- ^ Goodman, Joseph W (2005). Introduction to Fourier optics, 3rd edition. Greenwood Village, CO: Roberts and Company. pp. 26. ISBN 0974707724.
- ^ Nasse, H. H.. "From the Series of Articles on Lens Names: Tessar". Carl Zeiss AG.. http://www.zeiss.com/C12578620052CA69/0/58D501E36518AFC9C12578D2004104E1/$file/cln_39_en_tessar.pdf. Retrieved 19 December 2011.
- ^ http://www.dpreview.com/news/1109/11092119nikonJ1.asp#press
- ^ "Canon's Full Frame CMOS Sensors" (Press release). Canon. 2006. http://www.usa.canon.com/uploadedimages/FCK/Image/White%20Papers/Canon_CMOS_WP.pdf. Retrieved 2009-12-26.
- ^ "Kodak Announces Highest Resolution Image Sensors for Professional Photography" (Press release). Kodak. 2005-10-20. http://www.dpreview.net/news/article_print.asp?date=0510&article=05102101kodak_3936mpccd.
- ^ "The Phase One P+ Product Range". PHASE ONE. http://www.phaseone.com/en/Digital-Backs/P65/~/media/Phase%20One/Products/Documents/Phase-One-digital-back-overview.ashx. Retrieved 2010-06-07.
- ^ "Leica S2 with 56% larger sensor than full frame" (Press release). Leica. 2008-09-23. http://www.dpreview.com/news/0809/08092301_leica_s2.asp. Retrieved 2010-06-07.
- ^ "Pentax unveils 40MP 645D medium format DSLR" (Press release). Pentax. 2010-03-10. http://www.dpreview.com/news/1003/10031002pentax645d.asp. Retrieved 2010-12-21.
- ^ Pogue, David (2010-12-22). "Small Cameras With Big Sensors, and How to Compare Them". The New York Times. http://www.nytimes.com/2010/12/23/technology/personaltech/23pogue.html?ref=technology.
- ^ a b Bockaert, Vincent. "Sensor sizes". Digital Photography Review. http://search.dpreview.com/?q=sensor+sizes. Retrieved 2011-12-14.
- ^ Camera Sensor Ratings DxOMark
- ^ Imaging-resource: Sample images Comparometer Imaging-resource
- ^ Defined here as the ratio of the diagonal of a full 35 frame to that of the sensor format, that is CF=diag35mm / diagsensor.
- ^ KODAK KAF-39000 IMAGE SENSOR, DEVICE PERFORMANCE SPECIFICATION, April 21, 2010, http://www.kodak.com/global/plugins/acrobat/en/business/ISS/datasheet/fullframe/KAF-39000LongSpec.pdf
External links
- Eric Fossum, "Photons to Bits and Beyond: The Science & Technology of Digital Imaging", Oct. 13, 2011 (video of lecture)
- Joseph James, Equivalence
- Simon Tindemans, Alternative photographic parameters: a format-independent approach
- Compact Camera High ISO modes: Separating the facts from the hype (May 2007)
- The «Mass» of Pixels or the «Mess» of Pixels? at 6mpixel.org
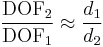
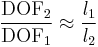
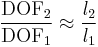
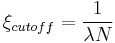
![{MTF}(\xi / \xi_{cutoff})=\frac{2}{\pi} \left \{ \cos^{-1}(\xi / \xi_{cutoff})-(\xi / \xi_{cutoff})\left [ 1-( \xi / \xi_{cutoff})^2 \right ]^{1/2} \right \}](/2012-wikipedia_en_all_nopic_01_2012/I/b08fe890759a33e8547db285e3c3e527.png)